Derived from the Latin sonus, historically the term resonance has been applied to sounds. A “resonant” voice for example is one that is deep, clear and “full of sound”. However, as we have learned more about the physical world around us we have come to understand that sound is a series of waves at differing frequencies and the principles of resonant sound apply generally to all things related to frequency.

It is generally accepted that, at birth, most humans can hear sound at frequencies from 20 Hz all the way up to 20 kHz. By definition anything outside of this range is not “sound” since it is not detectable by our hearing apparatus (ears). Nonetheless the frequency spectrum is continuous, starting at 0Hz and continuing on up to 600THz or so (though the sort of quantum effects generated by the Large Hadron Collider may go up even higher).

The problem that we run into once we are either above or below the audible range for humans, we must resort to other methods to measure the frequency; usually electrons or photons for ultrasound (above 20kHz). When we talk about sounds that are below 20 Hz (a realm known as infrasound), they usually have to be very powerful for us to sense them without special equipment. Usually they are felt, rather than heard. Examples are earthquakes, sonic booms, thunder, subwoofers and some whale vocalizations.

In sum, frequency is a fundamental property of matter and the means for generating and detecting the frequency of resonance of an object varies depending on its natural (or fundamental) frequency range. In our next section we’ll cover how and why engineers like to do vibration testing.

HOW RESONANCE WORKS

Most everything in this world has an inherent fundamental frequency that it likes to vibrate at. This varies according to the material, shape and size. This can be generalized to the simple formula that frequency, f = A*√K/M; where A is a constant to convert angular frequency to cycles per second (also known as Hertz), K is a fundamental constraint on the vibrating part (usually a major dimension or the stiffness of the vibrating part) and M is the mass of the vibrating object. For simple objects like a wine glass, a metal bar, or a guitar string for example you can just strike them with a hard object, and they will “ring” at their fundamental frequency. Another, more complex, but way more interesting way to make a physical object vibrate is to attach it to a mounting surface and make the mounting surface vibrate in a controlled fashion. In this way you can see what happens to the object both below and above its natural frequency. This is how engineers test parts to make sure they will last.

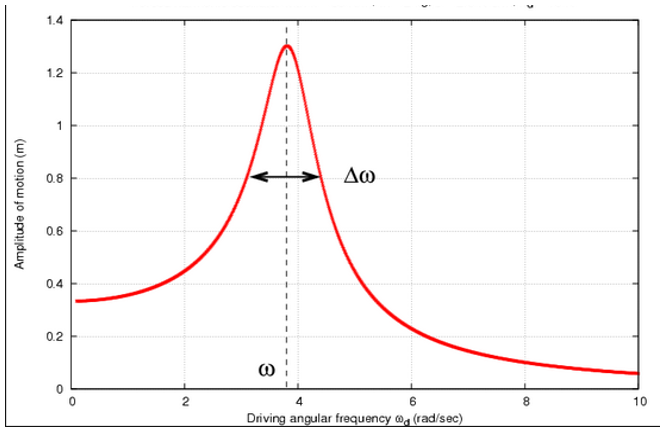
Now here is something interesting about this test. When the forced vibration (X-Axis) is less than the fundamental frequency, then the object being tested will vibrate at the forced frequency and at roughly the same amplitude (Y-Axis). As the forced frequency approaches the fundamental frequency, the amplitude of the vibration starts to increase rapidly. In fact, in some instances it increases so dramatically that it literally tears the piece apart. Above the fundamental frequency the amplitude decreases rapidly until it is well below the forcing amplitude. To the left (or above), you can see what this looks like in a graph form. So, next time you hear a whistle blow, a bell chime, someone tapping a wineglass, or the leaves of a tree twisting in a stiff breeze, these are all examples of how resonance oscillations are all around us. In our next section we’ll look at some unusual objects and the strange effects caused by their natural oscillations.

A FEW SURPRISES

Since virtually everything has a resonant frequency and there are a lot of “things” in the world it should come as no surprise that, from time to time two different objects will resonate “sympathetically” at the same frequency. Sometimes this has some very weird and/or dangerous effects. Perhaps one of the most famous is the galloping bridge over the Tacoma Narrows in 1940. A high cross wind excited the natural frequency of the bridge, and it created a mid-span oscillation like a series of waves crashing from one end to the other ref: https://youtu.be/j-zczJXSxnw eventually leading to collapse.

Researchers have long suspected that low frequency industrial infrasound could have deleterious effects. A recent study of studies was published in 2020 and indicated that prolonged exposure to low frequency (below the auditory threshold) sound could affect heart rate, create high levels of annoyance, and irritability, and higher blood pressure. Industrial noise examples are railways, oil and gas operations and wind turbine noise.

Riding comfort in long-haul truckers is a problem as well. Not just due to a large amount of sitting time, but the typical cab set-up has a natural frequency from 6.8 to 12 Hz and the internal body cavity organs of humans have resonant frequencies of 3 to 17Hz. This arrangement practically ensures that the heart, lungs, liver, spleen and kidneys get a thorough shaking up during the drive as well. Hopefully, newer cab designs will be forthcoming.

The average travel time of an earthquake shock is 60 minutes to travel to the other side of the globe and back. This equals 3600 seconds or a frequency of 0.00028 Hz. Analysis of large earthquakes (6.5 or greater) shows that for a three day period following such a jolt there is a significantly increased probability of other earthquakes (5.8 or greater) occurring. Earth rings like a bell after big earthquakes and there is enough energy in those vibrations, even a couple of days later, to shake a few more substantial earthquakes loose.

Oh, and lastly – you probably thought about the classic example of breaking a wine class with the power of your voice. Well, here’s a video to give you a satisfying ending to this little trip down resonance lane. https://youtu.be/Oc27GxSD_bI